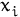Subject: Modeling
Problem*
Eli Daisy produces the drug Rozac from four chemicals. Today they must produce 1,000 lb of the drug. The three active ingredients in Rozac are A, B, and C. By weight, at least 8% of Rozac must consist of A, at least 4% of B, and at least 2% of C. The cost per pound of each chemical and the amount of each active ingredient in 1 lb of each chemical are given in the table below.
Chemical Cost ($/Lb) A B C 1 8 0.03 0.02 0.01 2 10 0.06 0.04 0.01 3 11 0.10 0.03 0.04 4 14 0.12 0.09 0.04 It is necessary that at least 100 lb of chemical 2 be used. Formulate an LP whose solution would determine the cheapest way of producing today's batch of Rozac.
* Source: Operations Research, W. L. Winston, 4th edition, Duxbury 2004. Page 93, Problem #11.
SOLUTION
Let
: Pounds of chemical used to produce 1000 pounds of drug
The LP model simply follows the given restriction and desired performance measure .
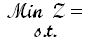
, , , The LINDO output for the problem is given below. Based on this solution, Eli Daisy should, for today's batch, use 285 of chemicals 1, 100 of chemicals 2, 417.5 of chemicals 3, and 197.5 pounds of chemicals 4 for today's mixture. The minimum production cost based on that solution is $10637.50.
MIN 8 X1 + 10 X2 + 11 X3 + 14 X4 SUBJECT TO 2) 0.03 X1 + 0.06 X2 + 0.10 X3 + 0.12 X4 >= 80 3) 0.02 X1 + 0.04 X2 + 0.03 X3 + 0.09 X4 >= 40 4) 0.01 X1 + 0.01 X2 + 0.04 X3 + 0.04 X4 >= 20 5) X1 + X2 + X3 + X4 = 1000 6) X2 >= 100 END LP OPTIMUM FOUND AT STEP 6 OBJECTIVE FUNCTION VALUE 1) 10637.50 VARIABLE VALUE REDUCED COST X1 285.000000 0.000000 X2 100.000000 0.000000 X3 417.500000 0.000000 X4 197.500000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 -37.500000 3) 0.000000 -37.500000 4) 8.450000 0.000000 5) 0.000000 -6.125000 6) 0.000000 -0.125000 NO. ITERATIONS= 6