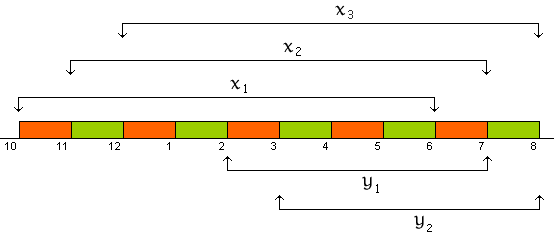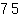Each hour from 10 A.M. to 7 P.M., Bank One receives checks and must process them. Its goal is to process all the checks the same day they are received. The bank has 13 check-processing machines, each of which can process up to 500 checks per hour. It takes one worker to operate each machine. Bank One hires both full-time and part-time workers. Full-time workers work 10 A.M.–6 P.M., 11 A.M.–7 P.M., or Noon–8 P.M. and are paid $160 per day. Part-time workers work either 2 P.M. -7 P.M. or 3 P.M.-8 P.M. and are paid $75 per day. The number of checks received each hour is given in the  table below. 

Period	Start Time	Checks
1	10am	5000
2	11am	4000
3	12pm	3000
4	1pm	4000
5	2pm	2500
6	3pm	3000
7	4pm	4000
8	5pm	4500
9	6pm	3500
10	7pm	3000

In the interest of maintaining continuity, Bank One believes it must have at least three full-time workers under contract. Develop a cost-minimizing work schedule that processes all checks by 8 P.M.

SOLUTION

Let
	:	Number of full-time employees starting at 10am
	:	Number of full-time employees starting at 11am
	:	Number of full-time employees starting at 12pm
	:	Number of part-time workers starting at 2pm
	:	Number of part time workers starting at 3pm

 

Graphically it can be illustrated as:

For any individual block of time, several things happen:

• a number of new checks arrive at the top of the hour,
• a number of unprocessed checks from previous hours is at hand,
• existing full time employees and part time workers process a number of check during the one hour period, and
• a number of checks will remain for the next period.

We can write a balance equation for one hour time period as follows:

new check arrivals unprocessed checks from previous time period
processed checks in this time period checks left unprocessed for the next period

The above is true for all periods.  However, note that the first period has no "unprocessed checks from previous period" and the last period has no "checks left unprocessed for the next period". Let's look at two sample periods and see how the equation will shape up.

Third Period (12pm-1pm)

new checks arrived at the start of period 1 = 5000
checks processed during period 1 = 500 X1
checks unprocessed during period 1 and left for period 2 = 5000 - 500 X1
new checks arrived at the start of period 2 = 4000
total checks at hand at the start of period 2 = 4000 + (5000 - 500X1) = 9000 - 500X1
checks processed during period 2 = 500 X1 + 500X2
checks unprocessed during period 2 and left for period 3 = 9000 - 500X1 - 500X1 - 500X2 = 9000 - 1000X1 -500X2
new checks arrived at the start of period 3 = 3000
total checks at hand at the start of period 3 = 3000 + (9000 + - 1000X1 - 500X2) = 12000 - 1000X1 - 500X2
checks processed during period 3 = 500 X1 + 500X2 +500X3
checks unprocessed during period 3 and left for period 4 = 12000 - 1000X1 - 500X2 - 500X1 - 500X2 -500X3 = 12000 - 1500X1 - 1000X2 - 500X3
Thus, it seems that we have a general form for the unprocessed checks remaining for the next period as follows:
total number of checks through that period
Example: 5000 + 4000 + 3000 = 12000
subtracted by
500(number of periods that full time employees have worked through that period)
Example: 500(3X1 + 2X2 + 1X3)
Resulting in:
12000 - 1500X1 - 1000X2 - 500X3

Let's see how that would work for another period.

Sixth Period (3pm-4pm)

Unprocessed checks remaining for the seventh period:
total number of checks through that period
5000 + 4000 + 3000 + 4000 + 2500 + 3000 = 21500
subtracted by
500(number of periods that full time employees have worked through that period)
500(6X1 + 5X2 + 4X3 + 2Y1 + 1Y2)
Resulting in:
21500 - 3000X1 - 2500X2 - 2000X3 -1000Y1 -500Y2

In similar fashion, at the end of last period we have,
35500 - 4000X1 - 4000X2 - 4000X3 -2500Y1 -2500Y2

To write the LP model, we start with the clear constraints, namely the check processing machines. At each period there total number of employees should at most equal to the number of machines. That cab written as several constraints (X1<=13, X1+X2<=13, etc.), or, just by stating that the time that we have the most employees working, their number should be less that the available machines (X1+X2+X3+Y1+Y2<=13). Also, in all periods, there must be at least one full time employee.  That means that for the first period and the last period we should have X1>=1 and X3>=1. Finally, we must clear all check at the end of the last period. That is 35500 - 4000X1 - 4000X2 - 4000X3 -2500Y1 -2500Y2 = 0 which after factoring out and simplification it will be 8X1 + 8X2 + 8X3 + 5Y1 + 5Y2 =75. The objective function is simply the sum of all employees salaries. 

		,		,		,		,

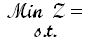
The LINDO output for the problem is given below. Note that problem was solved as an integer programming problem. Based on this solution, Bank One should hire 5 full time employees, 4 of whom to start work at 10am and the other one at 12pm.  Furthermore, they need to hire 7 part time employees all starting at 2pm.  The overall daily cost is $1325.  

    MIN     160 X1 + 160 X2 + 160 X3 + 75 Y1 + 75 Y2
  SUBJECT TO
         2)   X1 >=   1
         3)   X3 >=   1
         4)   X1 + X2 + X3 + Y1 + Y2 <=   13
         5)   8 X1 + 8 X2 + 8 X3 + 5 Y1 + 5 Y2 =    75
  END
  GIN      5
  
         OBJECTIVE FUNCTION VALUE

        1)      1325.000

  VARIABLE        VALUE          REDUCED COST
        X1         4.000000        160.000000
        X2         0.000000        160.000000
        X3         1.000000        160.000000
        Y1         7.000000         75.000000
        Y2         0.000000         75.000000


       ROW   SLACK OR SURPLUS     DUAL PRICES
        2)         3.000000          0.000000
        3)         0.000000          0.000000
        4)         1.000000          0.000000
        5)         0.000000          0.000000

 NO. ITERATIONS=     386 

Here is another solution offered by the author of the textbook.

Let
 PTi = Part-time people starting at i PM and
  Fi = Full-time people starting at hour i .
  
Also define
 INVi = checks that have arrived before hour i and are unprocessed at time i, and
  Pi = checks processed between time i and time i + 1.
  
Then a correct formulation is

Min z = 160(F10 + F11 + F12) + 75(P2 +P3)

s.t.  INV11 = 5000 – P10
       INV12 = INV11 + 4000 – P11
       INV1 = INV12 + 3000 – P12
       INV2 = INV1 + 4000 – P1
       INV3 = INV2 + 2500 – P2
       INV4 = INV3 + 3000 – P3
       INV5 = INV4 + 4000 – P4
       INV6 = INV5 + 4500 – P5
       INV7 = INV6 + 3500 – P6
       INV8 = INV7 + 3000 – P7
Pi<= 6500 (I = 10, 11, …7)
P10<=5000F10
P11<=5000(F10 + F11)
P12<=5000(F10 + F11 + F12)
P1<=5000(F10 + F11 + F12)
P2<=5000(F10 + F11 + F12 + P2)
P3<=5000(F10 + F11 + F12 + P2 + P3)
P4<=5000(F10 + F11 + F12 + P2 + P3)
P5<=5000(F10 + F11 + F12 + P2 + P3)
P6<=5000(F11 + F12 + P2 + P3)
P7<=5000(F12 + P3)
ALL VARIABLES >=0